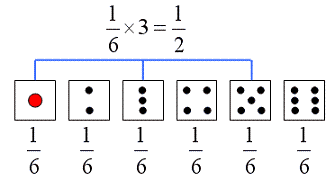
最大値が4以上の確率 大のサイコロは、 「4,5,6」の3通り 小のサイコロは、 「4,5,6」の3通り よって、 (3×3)/(6×6) · サイコロを1つ投げるとき、目の出方は 1,2,3,4,5,6 このように全部で6通りありますね。 この中から3の目は 1,2, 3,4,5,6 1通りしかありませんね。 だから、サイコロ1つを投げたとき、3の目が出る確率は $$\frac{1}{6}$$ となります。サイコロの確率 問題2 次の確率を考察せよ。 1個のサイコロを3回投げる。 (1)1の目が0回でる確率。 (2)1の目が1回でる確率。 (3)1の目が2回でる確率。 (4)1の目が3回でる確率。 (5)3回とも1の目がでない確率。 (6)3回目に初めて1の目がでる確率。

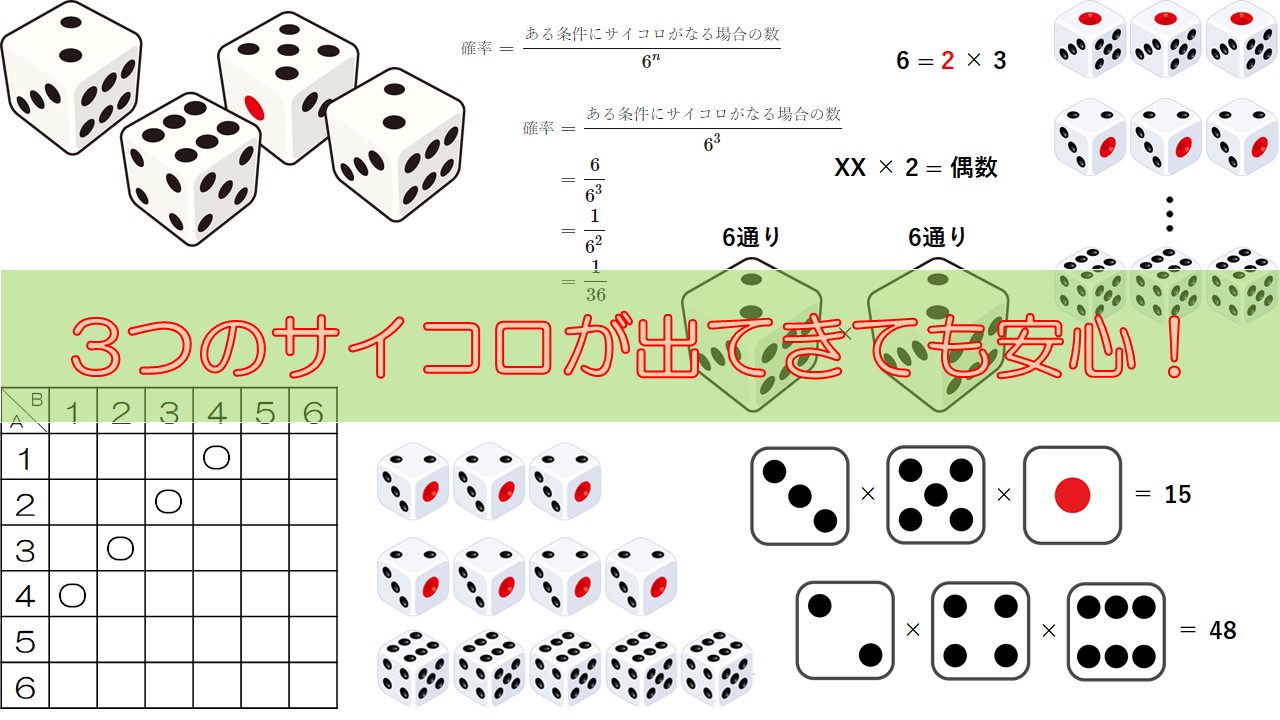
中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
確率 サイコロ 3つ
確率 サイコロ 3つ-詳細 確率の問題であれば、区別が必要です。なぜなら確率というのは「出やすさ」を求めることが目的であるためです。 例えば、2個のサイコロを同時に投げて、1・1と出るのは、両方のサイコロが同時に 1/6 という確率を引き寄せて初めて実現するものです。2110 · サイコロの目の積が3の倍数になるためには、3か6が1つ以上必要。 この問題では、余事象の方が少ないので余事象を求めます。 余事象=3も6もない場合 答え:19/27 別解 余事象の確率を求めます。 3つのサイコロ共に3,6以外の目が出る




3分動画 等確率 区別のない3つのサイコロ 数学a 確率 Youtube
結果と確率変数を区別したかったからである 例題 21 で各ローマ数字は各結果を表す 例えば, サイコロで偶数の目が出る事象を \(\{2, 4, 6\}\) と書いた場合, 暗黙にサイコロの目と確率変数を同一視している(そうでない場合の例が次にすぐ出てくる確率と確率変数 サイコロを投げ, 3か6の目が出たら出欠を取る 1,2,4,5の目が出たら出欠は取らない サイコロの目の全ての出方は Ω={1,2,3,4,5,6}←標本空間( sample space ) ©ATSUTO NISHIO 出欠を取るという事象 :E 1 ={3,6}例えば、サイコロを投げて出る目は{1, 2, 3, 4, 5, 6}のどれかです。 それぞれの目が出る確率は1/6ですから、 サイコロを投げて出る目は確率変数である と言えます。 この場合、確率変数の値(=サイコロの出る目)を「X」とすると、次のように表すことができます。 P (X)=1/6(X=1,2,3,4,5,6) 右側のカッコの中は「X」がとる値の範囲です。 簡単に言うと、 全部
サイコロの確率 ~各目の出る確率は本当に6 分の1なのか~ 研究者氏 ¡ 川戸口 雄太 尾﨑 優介 山田 時生 担当職員 澤柳 博文 1 研究の動機 ・ 私たちは、「サイコロの目」が凹んでいることに疑問を持った。確率の分布 311 確率変数 次の表は実際に1 つのサイコロを10 回投げて,それぞれの目が出た硬貨 の数(X)とその頻度数(F)を示します。 サイコロの目(X) 1 2 3 4 5 6 和(S) 実際の頻度(F) 2 2 1 0 3 2 10 このような表は度数分布表(frequency distribution)とよばれます。とる確率が最大になり,確率分布は Fig 2 の ようになります。 0 015 010 005 000 y S2 Fig 2 二つのサイコロを振ったときに出る目の和 S 2 の確率分布 三つのサイコロを振って出る目の和 S 3 は,3 から 18 までの値をとり,確率分布は Fig 3 のようになります。
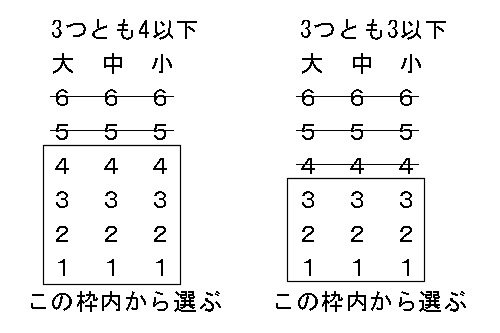
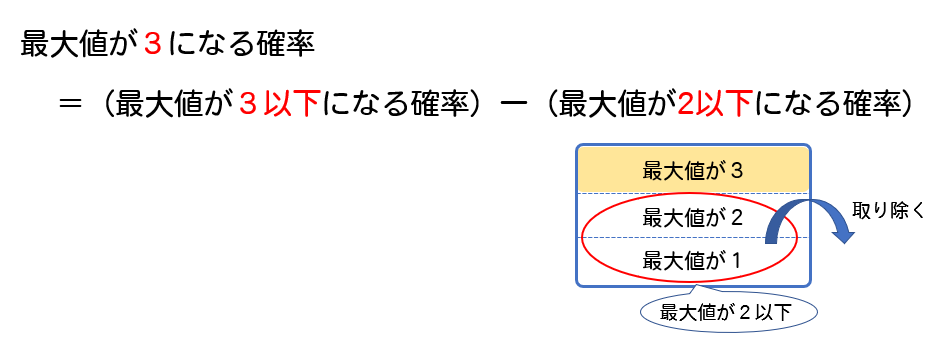
〔例題例題例題 51 51 51〕 3 個のサイコロを投げて出る目の最大値と最小値の確率分布を求めよ. (解)3 個のサイコロの出る目を,それぞれ X,Y,Z ,目の最大値を表す確率変数 を Xmax とする.このとき,次のことが成り立つ.確率の基本 ※数学Aで習う確率の初めの部分は,中学校の復習になっている. 確率の定義 例1 くじで当たる確率を求めるときに,「当たりかはずれかどちらかだから,当たる確率は2分の1」などと雑な議論をしてはいけない.さいころの目の最大値が3以下、3になる確率 4個のさいころを同時に投げるとき,次の確率を求めよ。 すべての目の出方は、 通りとなります。 あとで分数に形にして約分できることを考えて、 は計算せず、このままの形にしておきます。 どの目も (3通り)のどれかということになります。




サイコロ10コの出目の合計を当てろ やぐち建築士の備忘録




2つのサイコロの確率 Youtube
確率3 例1 サイコロを投げたとき奇数の目が出る確率 目の出方は 1,2,3,4,5,6 でN=6通り 奇数の目は 1,3,5 でn=3通り どの目の出方も同様に確からしいから 3 1 · サイコロ3つの目の和が5になる確率は、 (サイコロの目の和が5になる場合の数)÷(すべての場合の数) = 6÷216 = 36分の1 になるね。 おめでとう! 3つのサイコロの確率をマスターしたね^_^ まとめ:サイコロ3個の問題は根性と樹形図でとく! 3つのサイコロの問題は正直、 近道がな確率密度関数と累積分布関数 「確率変数 のとる値が 以下である」という事象とその確率を と表し、関数 を「 累積分布関数(または分布関数) 」 という つまり累積分布関数は、確率変数 が最小値から指定された値までをとる間の確率(最小値に対応




サイコロの確率の計算問題13選 2つ投げる場合の求め方とは 遊ぶ数学




1個のさいころを5回投げて目の和が10以下になる確率 怜悧玲瓏 高校数学を天空から俯瞰する
サイコロを1回投げるとき サイコロ投げ有限母集団説を採用する •母集団から1個 ランダムに取り出 し数字を確認す る作業を、x (確 率変数)とする。 1 2 3 4 5 6 母集団 割合はそれぞれ「6 分の1」である。 確率サイコロの目の和 組み合わせ(通り) 確率 確率(%) 3 1 4 3 0013 13 5 6 6 10 7 15 8 21 9 25 10事象 A が起こる確率が p のとき,この試行を 5 回繰り返して A が 3 回起こる確率は,次の各場合を足せばよい. (1) p p p q q = p 3 q 2 (2) p p q p q = p 3 q 2 (3) p p q q p = p 3 q 2 (4) p q p p q = p 3 q 2 (5) p q p q p = p 3 q 2 (6) p q q p p = p 3 q 2 (7) q p p p q = p 3 q 2 (8) q p p q p = p 3 q 2




この問題は サイコロ3つを区別してますか セットアップ Clear




素朴な疑問なのですが 5 6 6と6 6 6とあるのですが 150以上になる数が 6 Clear
(3) 無限回のサイコロ投げ 有限回だけサイコロを振る場合や根元事象の数が有限個のとき, (1), (2) で見たようにラプラス流の確率 で間に合う(根元事象の確率がすべて等しい場合も考えるというふうに一般化していますが) 何回も独立に0709 · サイコロの確率の問題です。 お祭りのチョコバナナの屋台で、 3つのサイコロを使って 1①②③か④⑤⑥がでれば2本、 2①①①などゾロ目なら3本 というものでした。ブログ http//kantaro1966net/blogentry1html「家族で行こう!自転車の旅」連絡先 kantaro@momosonetnejpeの本質 https//youtube/1M7FF1nd25I



数学を極める 1 確率を極める 予備校なら武田塾 河内松原校



Q Tbn And9gcszcyvszcu2ik9lg4f4f Cuh0aqhlmuilhm071xxcg6lctjjqo Usqp Cau
2つのサイコロの出る目の和の確率 2つのサイコロa,bを同時に振ったとき,出る目の和を算出し, すべての場合の数を数え,確率を求めよ. 表1 2つのサイコロの出る目の和の確率 シート確率の定義 上: 確率論の始まり 前: 同様に確からしい 確率は賭け事の理論 南海 このように「同様に確からしい」ということを考えたのは,もともとは賭け事にはじまる. まえに少し『数学対話』「何が同様に確からしいのか」で紹介したが,人間は昔から賭け事が大好きだ.0306 · 1 確率の問題です。 教えてください。 aさんはサイコロを3つ、bさんはサイコロを1つ投げる。aさんが投げ 2 3個のサイコロを同時に投げるとき、出た目の積が5の倍数になる確率を求め ;




中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



サイコロを2つまたは3つ以上振る確率の求め方と重複試行
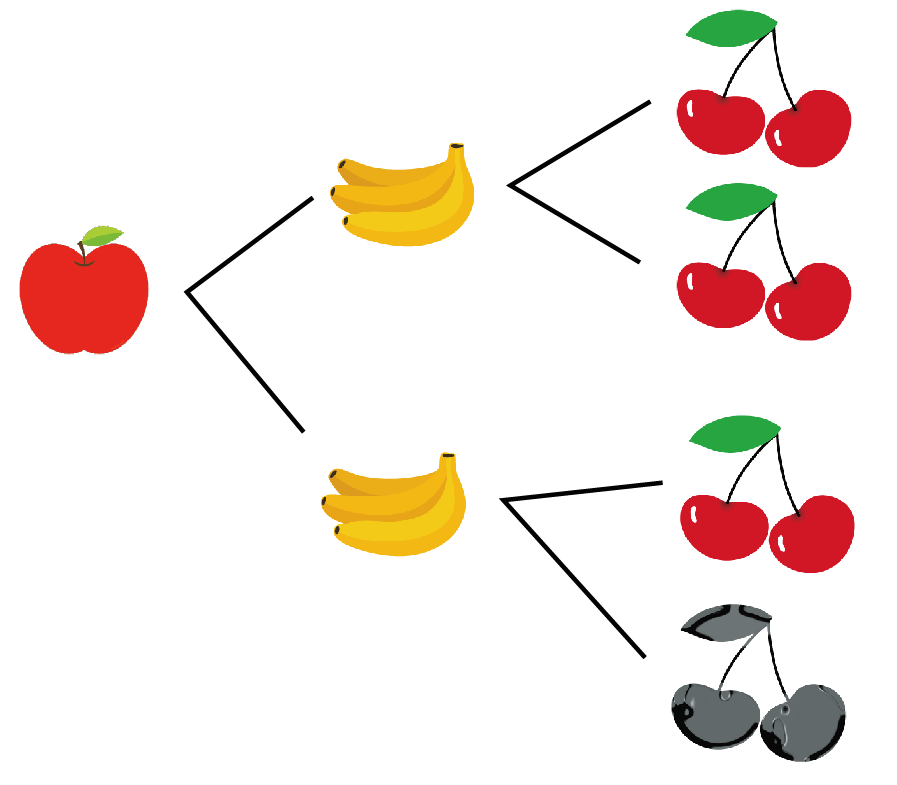
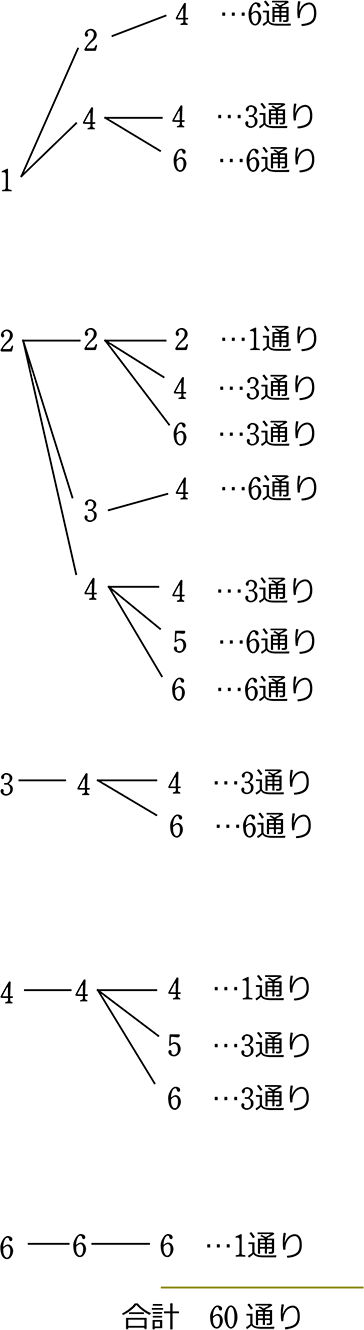
例えば、サイコロを3回振るとき、 「1回目奇数」「2回目偶数」「3回目奇数」 となる確率は、 \( p=\displaystyle \frac{1}{2}\times \displaystyle \frac{1}{2}\times \displaystyle \frac{1}{2}=\displaystyle \frac{1}{8}\) と求めることができるということです。 · 3つのサイコロを同時にふって、目が全て同じになる確率は? 3個のサイコロの目の出方は 6^3=216 通り 3つの目が全て同じになる組合せ (1,1,1) (2,2,2) (3,3,3) (4,4,4) (5,5,5) (6,6,6) の6通り よって6/216=1/36 これは幼稚な解答なので 数学的解説お願いします。問 区別のない 3 個のサイコロを投げるとき,出た目の和が 5 となる確率を求めよ.重複組合せ!




中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



サイコロを2つまたは3つ以上振る確率の求め方と重複試行
2301 · 数学 確率①3個のサイコロを同時に投げるとき、次のような目が出る確率は?1)3個の目の積が偶数 答え) 7/81)積が偶数なので、3つの内に1つ偶数が有れば良いつまり、(偶数なんでもなんでも)となるので、3/6 × 1 × 1 = 1/2 (答)1回試行で特定の目が出る確率 pのサイコロを n回の試行で特定の目が m回出る確率 Pは、 P = b i n o m i a l p d ( m , n , p ) = n C m p m ( 1 − p ) n − m P = b i n o m iそこで3枚のカードのうち, 6 だけを他の自然数が書かれたカードに交換して,点 p が頂点Aに移動する確率が0でないようにしたい。 どのような自然数が書かれたカードに交換すればよいか,その自然数について,言葉や数,式などを使ってすべての場合を説明せよ。



Ieubxdd1ge0dyb3c2crf51b4ejc3n Com Saikoro3 Html




Descubre Como Resolverlo En Qanda



中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学受験算数 サイコロ3つでも楽勝 和が6の倍数になる通り数を数えろ 毎日1題中学受験算数24 Youtube




サイコロの確率の計算問題13選 2つ投げる場合の求め方とは 遊ぶ数学




3分動画 等確率 区別のない3つのサイコロ 数学a 確率 Youtube



サイコロの確率の問題 京極一樹の数学塾




中学数学の確率の問題の解き方 コイン サイコロ くじ カード 数学fun



3個のさいころを同時に投げるとき目の和が7の倍数になる確率を求めよ という問 Yahoo 知恵袋




確率の計算 サイコロを投げる場合 数学の偏差値を上げて合格を目指す




高校の数学についてです 3つのサイコロを同時に投げた時 すべて異な 数学 教えて Goo




高校数学 数a 19 確率 さいころ編part 1 Youtube



一色パの難しさ パズドラ エクレア牧場




3個のさいころを同時に投げるときの確率の問題です Clear




中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト




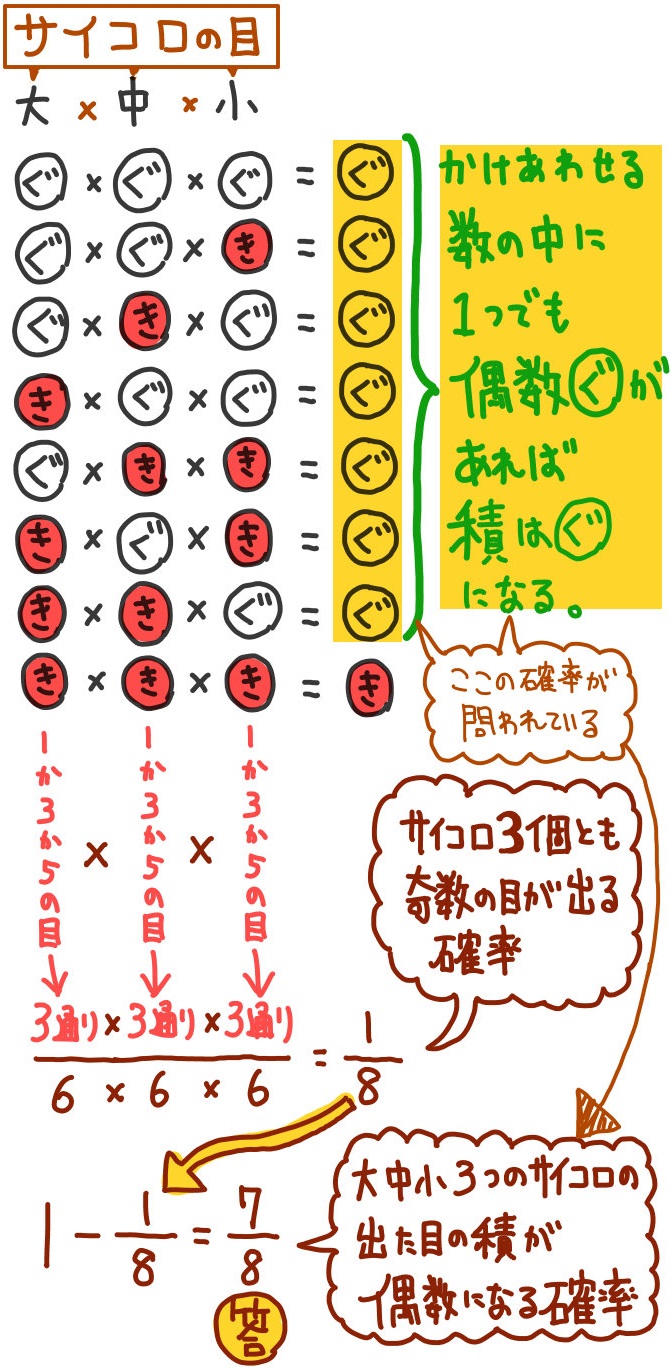
高校数学a 補集合の利用 でない 少なくとも サイコロの目の積が偶数 4の倍数 受験の月



数学 確率 解き方 サイコロ



簡単計算 2つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




中学数学の確率 コインとサイコロの問題の解き方と樹形図 リョースケ大学




北海道大18文系第3問 数ia確率 サイコロ3つで3ケタの数字を作る Mm参考書



数学教えてくださいq大中小三個のさいころを投げるとき 目の和 Yahoo 知恵袋



数学i Aチェック リピート 第8章 1確率とその基本性質 4 さいころの確率 Pukiwiki




3個のさいころの出る目の最小値 Youtube




中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学数学 確率



Ieubxdd1ge0dyb3c2crf51b4ejc3n Com Saikoro3 Html



サイコロの確率の練習問題 高校入試 中学数学 を難問まで難易度別に解説 坂田先生のブログ オンライン家庭教師の数学講師




中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト



中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




サイコロ3個を振った時の確立について質問です サイコロ3個を振っ 数学 教えて Goo




大 中 小3個のさいころを同時に投げるとき 1 3個とも同じ目が出る確率 Clear



3つのサイコロ




サイコロの出た目を使った三角形を作る確率の問題です 大学入試数学問題の解説 解答




中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




こういう解説があるのですが サイコロを区別とはどういう意味でしょうか Clear




大 中 小3個のさいころを投げるとき 次の場合は何通りあるか Youtube




条件付き確率とは 公式を使ってサイコロ 玉の問題を解いてみよう くじ引きを用いた例題付き 高校生向け受験応援メディア 受験のミカタ



Http Www Enjoymath Sakura Ne Jp 050 Z Hansha Baainokazukakuritu013saikoro3ko0601 C Utf8t Pdf



2




中学数学 さいころ2個の確率問題をパターン別に解説 数スタ



サイコロの目は予想できる 岡山モノポリークラブ




サイコロの出た目の最小公倍数の確率の問題です F1 数学 箱根駅伝ブログ




2つのサイコロを振ったとき 出易い合計数はあるか わけいブログ




サイコロを4回振る問題で 目の積が奇数でありかつ3の倍数になる確率 高校 教えて Goo




確率変数と確率分布の基本 さいころの例と確率分布のいろいろな例 Irohabook



中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト



中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト




2つのサイコロの目の合計が偶数になる確率の出し方 優しく教えて下さ 中学校 教えて Goo



簡単計算 2つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく




高校入試 さいころ 3個 の確率 Youtube



さいころ 球 カードの確率の問題 Of 京極一樹の数学塾会員頁



数学で 3個のサイコロを同時に投げるとき 次の確率を求めよ Yahoo 知恵袋
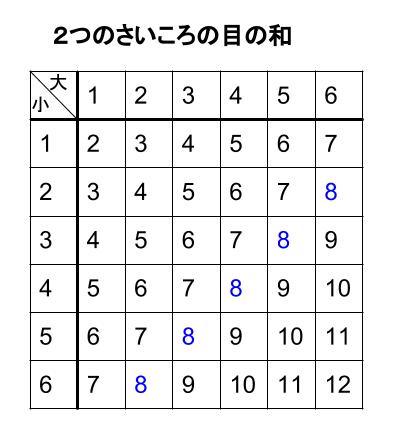



中学数学 確率 さいころ 中学数学の無料オンライン学習サイトchu Su



3つのサイコロ




サイコロの確率の計算問題13選 2つ投げる場合の求め方とは 遊ぶ数学



1
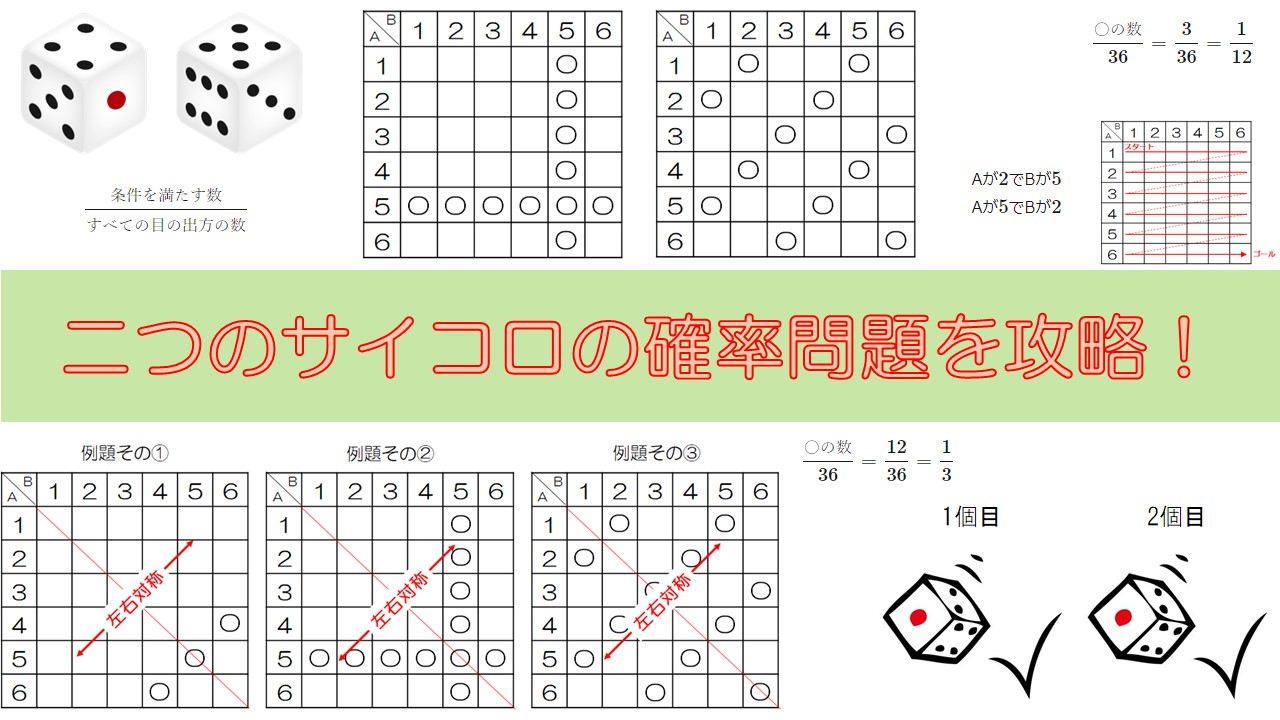



中学2年数学 確率 二つのサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト



3つのサイコロを振って1 2 3が出る確率と1 1 1が出る確率って同じ Yahoo 知恵袋




サイコロの和と多次元立方体の関係 小人さんの妄想




高校数学 数a 20 確率 さいころ編part 2 Youtube
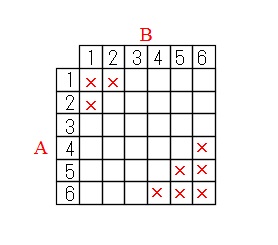



サイコロを2つまたは3つ以上振る確率の求め方と重複試行




N018 16 33 12 Left 1righ Descubre Como Resolverlo En Qanda




サイコロでゾロ目がでる確率を3秒で計算できる公式 Qikeru 学びを楽しくわかりやすく
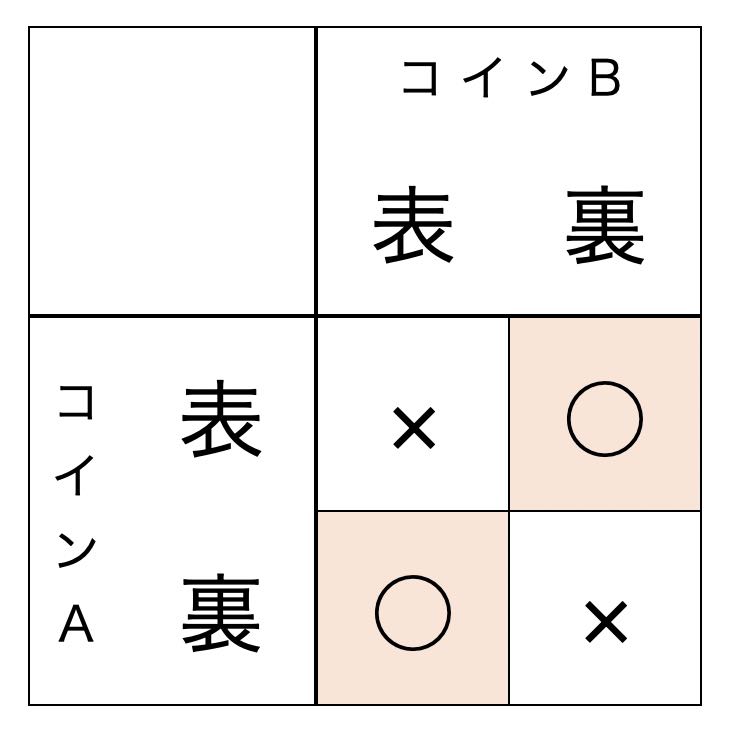



確率の計算ができないキミへ 数学a スタディクラブ情報局



3個のさいころを同時に投げるとき確率を求めよ 1 3個の目 Yahoo 知恵袋




反復試行



13 Introduction To Experimental Mathematics Ii By D Furihata



5 3 確率サイコロ 日立市民科学文化財団
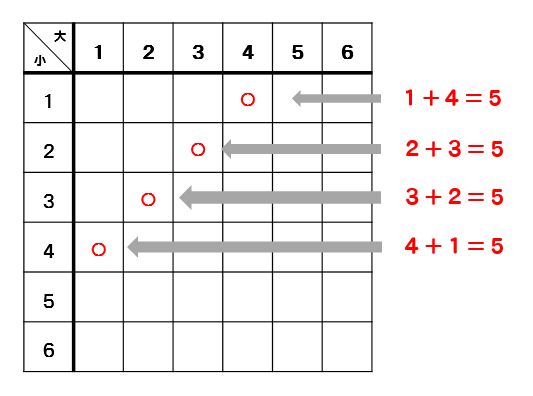



中学数学 さいころ2個の確率問題をパターン別に解説 数スタ




場合の数 大中小3つのサイコロを投げるとき何通り 奇数 偶数 4の倍数 数スタ



1




高校数学a 反復試行の確率 基本 Ncrp R 1 P N R 受験の月



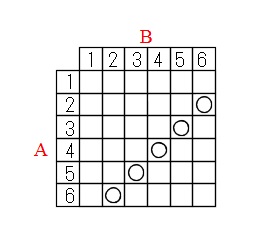
大中小3つのさいころを同時に投げるとき 目の和が15以上になる場合は何 Yahoo 知恵袋




なぜこのときさいころ3個を区別しないで考えるのでしょうか Clear



中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト




後編 サイコロ3つのうち1 2個の出目を当てる 大小 シックボー の確率と配当まとめ カジラグ




非推移サイコロ3つ ジッヒャーマンダイス 確率論のサイコロ 発明 発見 年表
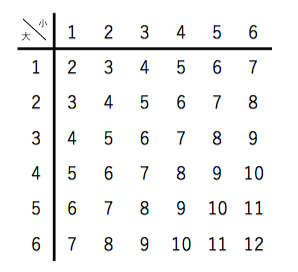



確率の基本 サイコロを投げる 苦手な数学を簡単に




数学a 大中小の3個のサイコロを投げる時 出る目が全て異なるときの確 高校 教えて Goo



サイコロの確率の問題 京極一樹の数学塾



確率は賭け事の理論



中学2年数学 確率 3つ以上のサイコロが出てくる確率の問題を攻略しよう 数学の面白いこと 役に立つことをまとめたサイト




株 日科技研 第24話 インドサイコロの確率計算 六一学者の千字一話 会員広場




さいころを2個同時に振ったとき 8なる確立 立方体のさいころを2個同 数学 教えて Goo



3つのサイコロを同時に振ります 3つとも違う目が出る確率はいく Yahoo 知恵袋
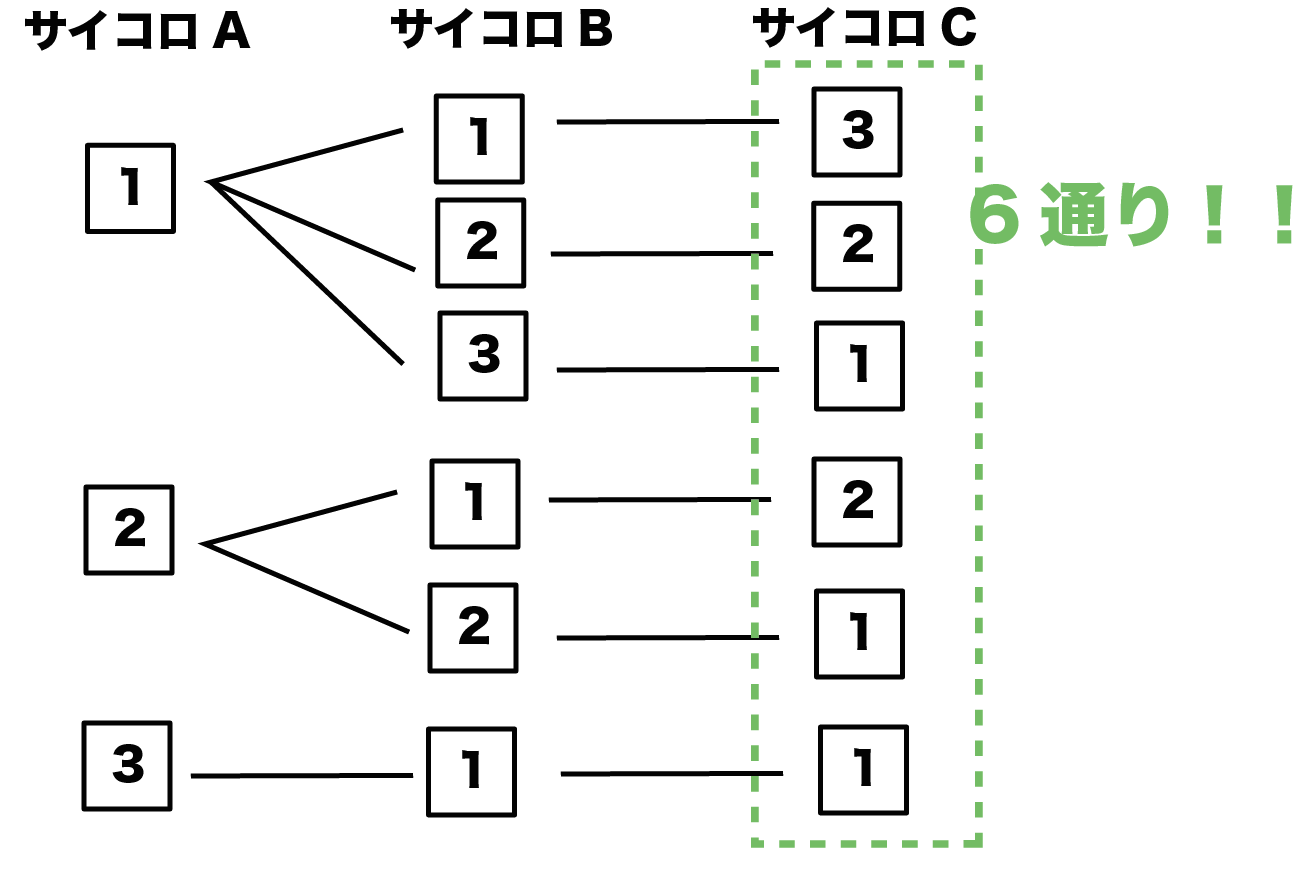



中学数学 3つのサイコロの確率の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



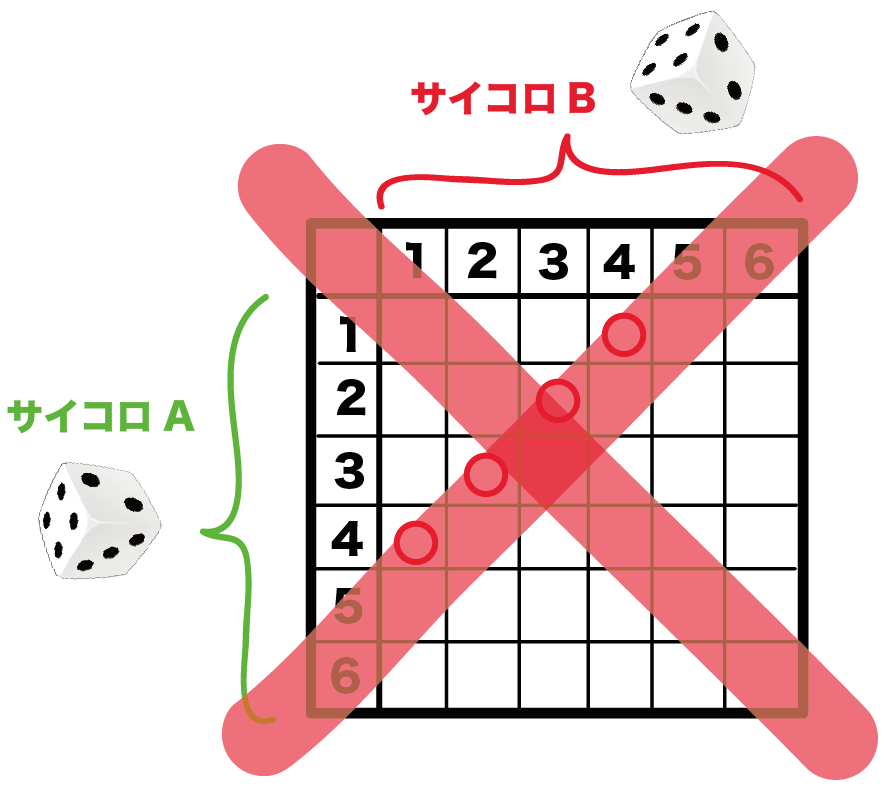
数学a サイコロの最大値が5 最小値が2になる確率はどうやって考える 数スタ




3 を教えてください Clear



数aサイコロの確率42の2と3の解説お願いします 4個のサイコロ Yahoo 知恵袋




反復試行の確率 3つの事象があるときのやり方は 数スタ



0 件のコメント:
コメントを投稿